Apakah algoritma sorting itu? berdasarkan
wikipedia Algoritma Sorting merupakan algoritma yang menempatkan elemen list
pada urutan tertentu. Urutan yang paling sering digunakan ialah urutan
numerikal. Sorting yang efisien sangat dibutuhkan untuk mengoptimisasi
penggunaan dari algoritma lain seperti pencarian dan penggabungan yang
membutuhkan list terurut untuk berjalan dengan sempurna.
Proses Sorting itu tidak akan tampak
perbedaannya jika data yang Anda sorting itu masih sedikit. Bagaimana kalau
Anda sorting Data perusahaan yang jumlahnya itu bisa beribu – ribu banyaknya
bahkan berjuta – juta. Apa mau si user menunggu waktu 1 jam lebih atau 1 harian
penuh hanya untuk menunggu proses sorting selesai sementara di sisi lain dia
bisa mendapatkan hal yang lebih bagus dari itu yakni cukup 10 menit data akan
terurut dengan benar. Nah, di sinilah pentingnya dari proses Algoritma.
Tujuannya sama – sama untuk mengurutkan namun, dari segi kecepatan algoritma
jelas berbeda.
Disini akan saya jelaskan tentang insertion
sort dan merge sort.
1. Insertion Sort
1. Insertion Sort
Insertion Sort merupakan metode pengurutan
dimana langkah – langkah ialah membandingkan dari data kedua ke data pertama
(Data-N <==> Data-N-1). Berbeda dengan Bubble Sort dimana, proses
perbandingannya dimulai dari Data Pertama sampai Data Terakhir.
Untuk lebih jelasnya langsung masuk ke contoh kasus.
Untuk lebih jelasnya langsung masuk ke contoh kasus.
Data : 11 8 2 22 29 1
Proses Insertion Sort (Ascending)
Iterasi 1:
11
8 2 22
29 1 → (Bandingkan Data 8 dengan
11)
8
11 2 22
29 1 → (Tukar Data 8 dengan 11)
Iterasi 2:
8 11 2
22 29 1 → (Bandingkan Data 2 dengan 11)
8
2 11 22
29 1 → (Tukar 2 dengan 11.
Bandingkan 2 dengan 8)
2
8 11 22
29 1 → (Tukar 2 dengan 8)
Iterasi 2:
2
8 11 22
29 1 → (Bandingkan 22 dengan 11)
2
8 11 22
29 1 → (Tidak ada pertukaran)
Iterasi 4:
2
8 11 22
29 1 → (Bandingkan 29 dengan 22)
2
8 11 22
29 1 → (Tidak ada pertukaran)
Iterasi 5:
2
8 11 22
29 1 → (Bandingkan 1 dengan 29)
2
8 11 22
1 29 → (Tukar 1 dengan 29.
Bandingkan 1 dengan 22)
2
8 11 1
22 29 → (Tukar 1 dengan 22.
Bandingkan 1 dengan 11)
2
8 1 11 22 29 → (Tukar 1 dengan 11.
Bandingkan 1 dengan 8)
2
1 8 11 22 29 → (Tukar 1 dengan 8.
Bandingkan 1 dengan 2)
1
2 8 11 22 29 → (Tukar 1 dengan 2)
Penjelasan Proses Insertion Sort (Ascending)
- Dalam Insertion Sort jumlah iterasi ialah
sebanyak jumlah data – 1. Untuk kasus diatas, Jumlah Data ialah 6 maka, jumlah
iterasinya ialah 6 – 1 = 5. Dan jumlah iterasi tersebut harus terpenuhi
walaupun Data sudah terurut.
- Setiap Iterasi memiliki proses dan jumlah
proses tersebut tidak bisa ditentuin karena, proses akan berhenti jika Data
sudah terurut. Bisa Anda lihat pada iterasi ke-2 dan ke-4. Pada iterasi 2 dan 4
proses pengecekannya cuma sekali namun, karena Data yang di cek memang sudah
terurut dengan benar maka, proses pengecekan berhenti dan lanjut ke iterasi
berikutnya.
- Untuk iterasi ke-1, Proses perbandingan
dimulai dari Data ke-2 dengan Data ke-1 (8 <==> 11). Karena, 8 < 11
maka, 8 tukar posisi dengan 11.
- Untuk iterasi ke-2, Proses perbandingan
dimulai dari Data ke-2 dengan Data ke-2 (2 <==> 11). Karena, 2 < 11
maka,2 tukar dengan 11. Selanjutnya, bandingkan lagi 2 dengan 8 (2 <==>
8). Karena 2 < 8 maka, 2 tukar dengan 8.
- Untuk iterasi ke-3, Proses perbandingan
dimulai dari Data ke-4 dengan Data ke-2 (22 <==> 11). Karena, 22 > 11
maka, tidak ada pertukaran. Posisi tetap tidak ada perubahan.
- Untuk iterasi ke-4, Proses perbandingan
dimulai dari Data ke-5 dengan Data ke-4 (29 <==> 22). Karena, 29 > 22
maka, tidak ada pertukaran. Posisi tetap tidak ada perubahan.
- Untuk iterasi ke-5, Proses perbandingan
dimulai dari Data ke-6 dengan Data ke-5 (1 <==> 29). Karena, 1 < 29
maka, 1 tukar posisi dengan 29. Selanjutnya,
bandingkan lagi 1 dengan 22 (1 <==> 22). Karena, 1 < 22 maka, 1 tukar
posisi dengan 22. Selanjutnya, bandingkan lagi 1 dengan 11 (1 <==> 11).
Karena, 1 < 11 maka, 1 tukar posisi dengan 11. Kemudian, bandingkan lagi
antara 1 dengan 8 (1 <==> 8). Karena, 1 < 8 maka, 1 tukar posisi dengan
8. Berikutnya, bandingkan lagi 1 dengan 2 (1 <==> 2). Karena, 1 < 2
maka, 1 tukar posisi dengan 2.
Dan Data setelah di sort adalah seperti
berikut.
Data: 1 2 8 11 22 39
Tidak terlalu susah kan? Konsepnya hampir sama
seperti Bubble Sort hanya saja di Insertion Sort proses dimulai dari Data kedua
(Data-N+1) dan di cek satu per satu ke Data sebelumnya(Data-N-1). Selain itu,
prosesnya juga berbeda antara Bubble Sort dan Insertion Sort. Kalau di Bubble
Sort jumlah proses tiap iterasinya selalu dikurang 1 sementara di Insertion
Sort jumlah prosesnya akan terus bertambah apabila Data tersebut masih bisa
ditukar.
Untuk lebih memudahkan perhatikan animasi
berikut:
source code untuk insertion sort:
public class insertion {
public int[]data;
public insertion(int n){
this.data=new int[n];
}public void setdata(int index,int value){
this.data[index]=value;
}public void print(){
System.out.print("data: ");
for (int i = 0; i < this.data.length; i++) {
System.out.print(this.data[i]+" ");
}
}public void tukar(int i,int j){
int c = this.data[i];
this.data[i]=this.data[j];
this.data[j]=c;
}public void sort(){
for (int i = 1; i < data.length; i++) {
int j =i;
while(j>0&&this.data[j]<this.data[j-1]){
tukar(j,j-1);
j--;
}
}
}public static void main(String[] args) {
insertion ins = new insertion(6);
ins.setdata(0, 11);
ins.setdata(1, 8);
ins.setdata(2, 2);
ins.setdata(3, 22);
ins.setdata(4, 29);
ins.setdata(5, 1);
ins.print();
ins.sort();
System.out.println("");
ins.print();
}
}
output:
2. Merge Sort
Merge Sort adalah algoritma pengurutan dalam
ilmu komputer yang dirancang untuk memenuhi kebutuhan pengurutan atas suatu
rangkaian data yang tidak memungkinkan untuk ditampung dalam memori komputer
karena jumlahnya yang terlalu besar. Algoritma ini ditemukan oleh John von
Neumann pada tahun 1945.
Algoritma pengurutan data merge sort dilakukan
dengan menggunakan cara memecah kemudian
menyelesaikan setiap bagian kemudian menggabungkannya kembali. Pertama data
dipecah menjadi 2 bagian dimana bagian pertama merupakan setengah (jika data
genap) atau setengah minus satu (jika data ganjil) dari seluruh data, kemudian
dilakukan pemecahan kembali untuk masing-masing blok sampai hanya terdiri dari
satu data tiap blok.
Setelah itu digabungkan kembali dengan membandingkan pada blok yang sama apakah data pertama lebih besar daripada data ke-tengah+1, jika ya maka data ke-tengah+1 dipindah sebagai data pertama, kemudian data ke-pertama sampai ke-tengah digeser menjadi data ke-dua sampai ke-tengah+1, demikian seterusnya sampai menjadi satu blok utuh seperti awalnya. Sehingga metode merge sort merupakan metode yang membutuhkan fungsi rekursif untuk penyelesaiannya.
Setelah itu digabungkan kembali dengan membandingkan pada blok yang sama apakah data pertama lebih besar daripada data ke-tengah+1, jika ya maka data ke-tengah+1 dipindah sebagai data pertama, kemudian data ke-pertama sampai ke-tengah digeser menjadi data ke-dua sampai ke-tengah+1, demikian seterusnya sampai menjadi satu blok utuh seperti awalnya. Sehingga metode merge sort merupakan metode yang membutuhkan fungsi rekursif untuk penyelesaiannya.
Untuk lebih jelasnya langsung masuk ke contoh
kasus.
Data: 11 8 2 22 29 1
- Pertama kali larik tersebut dibagi menjadi dua
bagian, {11, 8, 2} dan {22, 29, 1}
- Kedua larik kemudian diurutkan secara terpisah
sehingga menjadi {2, 8, 11} dan {1, 22, 29}
- Sebuah larik baru dibentuk yang sebagai
penggabungan dari kedua larik tersebut {1}, sementara nilai-nilai dalam masing
larik {2, 8,
11} dan {22, 29} (nilai 1 dalam elemen
larik ke dua telah dipindahkan ke larik baru)
- Langkah berikutnya adalah penggabungan dari
masing-masing larik ke dalam larik baru yang dibuat sebelumnya secara berurut.
Untuk lebih memudahkan perhatikan animasi berikut:
source code untuk insertion sort:
public class merge {
public int[]data;
public merge(int n){
this.data=new int[n];
}public void setdata(int index, int value){
this.data[index]=value;
}public void print(){
System.out.print("data: ");
for (int i = 0; i < this.data.length; i++) {
System.out.print(this.data[i]+" ");
}
}public void sort(){
int i=0;
int j=this.data.length-1;
mergesort(i,j);
}public void mergesort(int start,int end){
int n =(end-start+1);
if(n>1){
int mid=(start+end)/2;
mergesort(start,mid);
mergesort(mid+1,end);
int[]temp=new int[n];
int x = start;
int y = mid+1;
for (int i = 0; i < n; i++) {
if(x<=mid&&y<=end){
if(this.data[x]<this.data[y]){
temp[i]=this.data[x];
x++;
}else{
temp[i]=this.data[y];
y++;
}
}else if(x<=mid){
temp[i]=this.data[x];
x++;
}else{
temp[i]=this.data[y];
y++;
}
}for (int i = 0; i < n; i++) {
this.data[start+i]=temp[i];
}
}
}public static void main(String args[]){
merge m = new merge(6);
m.setdata(0, 11);
m.setdata(1, 8);
m.setdata(2, 2);
m.setdata(3, 22);
m.setdata(4, 29);
m.setdata(5, 1);
m.print();
System.out.println("");
m.sort();
m.print();
}
}
Output:

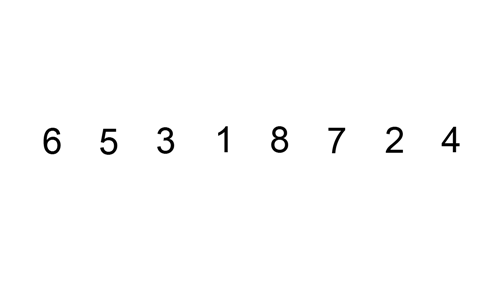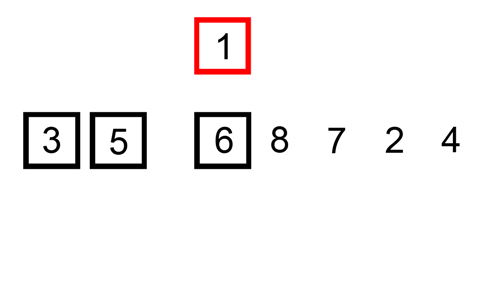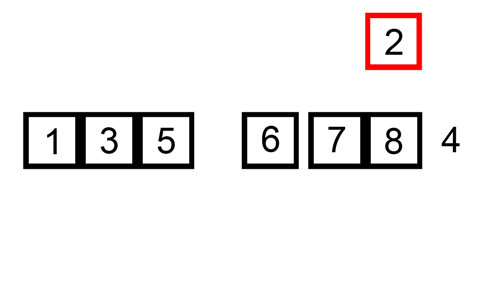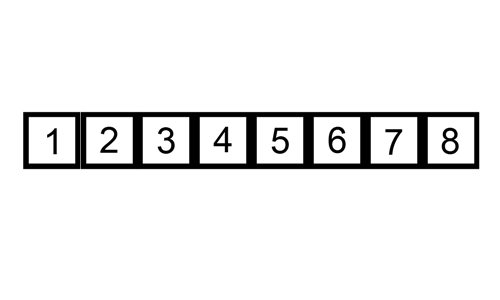




No comments:
Post a Comment